In the following mathematical content, we will cover the basics of the remainder theorem, its proof, and related examples. Moreover, we will also let you know how you can resolve complicated remainder theorem problems using the remainder theorem calculator.
Let’s get into it!
What Is the Remainder Theorem?
In mathematics,
The Euclidean division of the polynomials is known as the remainder theorem.
Proper Statement for Remainder Theorem
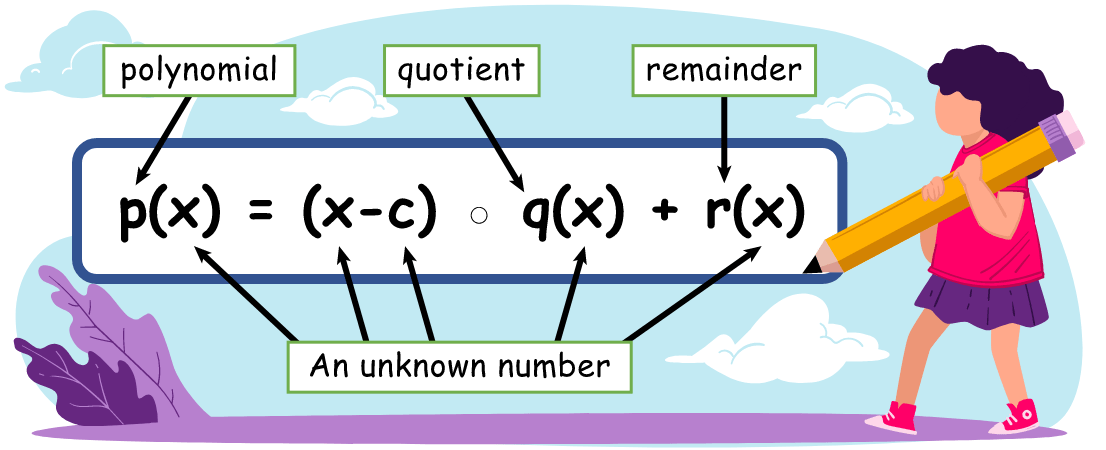
If we divide a polynomial in the form f(x) by x-a (a linear factor), then we will always get the answer in the form of a remainder.
The free remainder theorem calculator also works on the same scenario and calculates the remainder of polynomial divisions in seconds.
Let’s have a look at the proof of the theorem now!
Remainder Theorem Proof
Now suggest that we have the quotient and remainder of the polynomial division as q(x) and r, respectively. This is obtained when we divide a polynomial p(a) by a linear factor which is x-a.
According to the basic division formula, we have
Division=(Divisor*Quotient)+Remainder
We will use the same basic equation and put in our polynomial values:
p(x)=(x-a)*q(x)+r
Putting x=a in the above expression;
p(a)=(a-a)*q(a)+r
p(a)=(0)*q(a)+r
p(a)=r
Which satisfies the statement of the remainder theorem and is also utilized by the remainder theorem calculator to perform calculations instantly.
Important notes for Remainder Theorem!
Always remember that
- The Remainder theorem only calculates the remainder. You can not determine the quotient of division through it
- You will always get the remainder as p(k) if you go by dividing the polynomial p(x) by another linear polynomial having x as zero
- The basic formula to check the remainder and the quotient in the case of the remainder theorem application will always be the same as discussed above
- Another point of consideration is that you will never get the results by the remainder theorem if the divisor polynomial is not linear
Example Calculations with Remainder Theorem Calculator!
In the following section, we will be resolving a couple of examples of the concept under study. So stay focused!
Statement 01
Find the remainder of the polynomial p(x)=x3+5×2-2x+1 is divided by the linear polynomial x-2
Solution
The given polynomial is
p(x)=x3+5×2-2x+1
The linear factor is x-2
From this, we have
x-2=0=>x=+2
Putting the value of x in the bigger polynomial expression
p(x)=x3+5×2-2x+1
p(x)=23+5*22-2*2+1
p(x)=8+20-4+1
p(x)=15
Which is the required remainder of the division. For verification, you can also put in the values in the remainder calculator and justify your results. This online tool has provided another edge in calculations to mathematicians!
Statement 02
If you have the polynomial p(x)=x4-x3-x2+x+0 and you have to divide it by the linear polynomial x+5, what would be the remainder of the results?
Solution
As the given polynomial is
p(x)=x4-x3-x2+x+0
From the linear polynomial x+5, we have
x+5=>x=-5
Putting this value in the bigger polynomial to calculate the results
p(x)=x4-x3-x2+x+0
p(x)=-54+53+5-5+0
p(x)=625+125+5-5+0
p(x)=750
Statement 03
Determine the remainder of the polynomial division if the two algebraic polynomials are as follows
p(x)=3×3+2×2-x+2 divided by x2+1
Solution
Sorry, as you see that the divisor polynomial is not a linear one, it is impossible to apply the remainder theorem in this condition. Even if you enter the two expressions in the remainder theorem calculator, you are going to get an error for sure.
A Glimpse At Remainder Theorem Calculator
As we are discussing the use of the free calculator by the calculator-online.net site, we will be glad to let you know how you could use it!
- Just land on the official site of calculator-online.net
- Now type in Remainder theorem calculator in the search bar
- After the tools open on your screen, type in the polynomial and the factor in their respective fields and tap on the calculate button
- The tool will readily perform calculations and provide you with the results in seconds.
Faqs
What is the limitation of the remainder theorem?
The main drawback of the remainder theorem is that you can only use it to divide polynomials that contain integer coefficients. In case there is any complex number like iota 𝜾, you will not get the results you are looking for.
Why do we need the remainder theorem?
As a mathematician, we always need the remainder theorem to confirm whether the linear factor satisfies the polynomial or not. If we get the answer as zero, it satisfies, otherwise, it does not!
Can the remainder be negative in polynomials?
Yes, of course!
Wrapping It Up:
If you are struggling with algebra as a beginner, the following article will assist you in getting a firm grip on the technique of the remainder theorem. Moreover, the instant calculations provided by the remainder theorem calculator will also help you a lot in understanding the science behind calculations.